Equiripple linear-phase FIR filter (Remez / Parks–McClellan algorithm)

Introduction

The Parks–McClellan algorithm, is an iterative algorithm for finding the optimal linear-phase FIR filter. It is a variation of the Remez exchange algorithm designed for Finit Impulse Response (FIR) filters.

If the filter type selector in the DSP filter dialog is on Equiripple FIR and you click on the design button beside, the dialog box that allows you to configure and generate such a linear phase filter opens.

Here we briefly describe the Parks–McClellan algorithm in term of the frequency
ν = ω∙sampleRate ∕ (2∙π) instead of the angular frequency ω ( 0 < ω < π) because it is the x-coordinate used in the DSP dialog plot used for the illustrations.

The goal of the algorithm is to find a function A(ν) that minimize the difference with an ideal frequency response H(ν).

H(ν) is defined by its low and high edge frequencies ν_li and ν_hi and its gain H_i. For each band i of the filter whose number of bands is nBand:
H(ν) = H_i for ν_li < ν < ν_hi.

The space between two consecutive bands is the cutoff band and the cutoff width is
ν_l(i+1) − ν_hi, 0 ≤ i ≤ nBand -1.
⚠ There is no constraint on H(ν) for ν value inside a cutoff band.

The error function that has to be minimized is defined as:
E(ν) = H(ν) - A(ν).

The gains H_i, low and high edge frequency values ν _li and ν_hi can be set in the band parameters. If Debug is checked, E(ν) and A(ν) are the red and blue curves in the DSP dialog.

The function A(ν) is defined by its alternations that include its extremals (maxima and minima) represented by red dots in the plots and edge frequencies represented by red crosses. Actually, extremals plotted in the figures are not those used to define the function A(ν) but the extremals of the function defined during the previous iteration. Iteration stops when the extremals found correspond to the ones used for the definition and, in most of the cases, they all have the same amplitude. It can occur that iteration stops with some extremals having a larger amplitude. In that case, we call the solution frozen instead of converged which means that the convergence criteria is satisfied.

⚠ When the total number of alternations comes up to 1000, numerical errors becomes too large and the algorithm will fail searching for extremals or even compute δ. This is a current limitation of the 64-bit floating point implementation.

Implementation

The Remez exchange / Parks-McClellan algorithm implementation used here conists in:

Create an initial function A(ν) from guess on N alternation frequencies.
Calculate δ that is a parameter of the A(ν) definition computed from alternation frequencies. When convergence is reached, A(ν) is equiripple and δ is the the common ripple (extremal) amplitude and the tolerance of the filter.
Search the extremals of the error function. Here we use a customized Newton search instead of the fine grid method commonly used. It provides more accurate computation of extremals while requiring less E(ν) calculations.
If more than N alternations are found, retain N (most often the largest ones). If less than N alternations are found, the algorithm has failed and stops.
Check convergence criteria. Stop iterate if it is satisfied or the solution is frozen, go to step 2 otherwise.
If solution is converged, calculate the impulse response that is the inverse Fourier transform of A(ν) and the filter coefficients. The corresponding filter is a Type 1 linear-phase FIR filter that has a symmetric impulse response with odd length (even order). It is the only of the 4 types that has no constraints on H(0) and H(Nyquist).

The tolerance scheme

The filter ideal response H(ν) and tolerance δ constitute the tolerance scheme.
If Scheme is checked It is displayed in the DSP dialog.

Bands are separated by vertical green lines drawn at edge frequencies.

The middle horizontal green lines in the plot correspond to the H_i values. In dB scale it is 20 log₁₀(H_i) In the example, H₂=0.1 and the central band is at ∣H∣ = -20 dB. The upper and lower horizontal green lines correspond to H_i + δ and H_i − δ. If it is the initial solution, target δ is used instead of δ. In the example, the initial solution (first slide: It=0) for the central band has upper and lower limits at ∣H∣ = 20 log₁₀(0.1 + 5.012 10^-2) ∼ -16.5 dB and ∣H∣ = 20 log₁₀(0.1 − 5.012 10^-2) ∼ -26 dB. For the converged solution (second slide) δ = 8.56 10 ^-2 which gives upper and lower limits for the central bands at ∼ -14.6 dB and ∼ -36.8 dB.

The equiripple FIR design dialog

The following dialog opens when you click on the design button beside the DSP filter type selector when the selected type is Equiripple FIR.

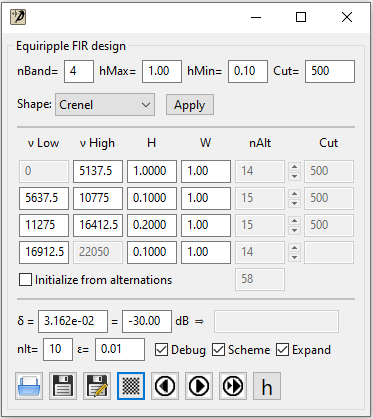
Global parameters

The top of the Equiripple FIR design dialog allows you to quickly design a filter with up to 12 bands. The resulting design is displayed below in the dialog box and the tolerance scheme is plotted in the DSP dialog after clicking on the Apply button.

The nBand entry sets the number of bands (2 ≤ nBand ≤ 12). ⚠ It is more difficult to obtain a converged solution that fits your requirements with a greater number of bands.
The hMax entry sets the highest value for the frequency response (gain) of the band.⚠ The filter order increases with hMax. The hMin value sets the lowest gain value.
The Cut sets the cutoff width between all bands of the initial design.
The Shape combobox allows you to select the shape of the initial design you can modify later
- Crenel as in the example where hMax and hMin values alternate.
- Up-stairs where the first band has a hMin gain and the last band hMax. The gain difference between two consecutive bands constant in the dB scale. That is why hMin is replaced by δ when hMin < δ since the log function is not defined in 0.
- Down-stairs is similar to Up-stairs but the first band has a hMax gain and the last band hMin.

When the number of bands or the filter order increase, you may need to search a bit for finding compatible values for δ, the cutoff width and hMax. Indeed, small delta or large hMax require a large number of alternations in the frequency response. These are therefore closely spaced and the algorithm will not find solution if the cutoff width and the gain difference between two consecutive band are large.

Band parameters

Each line has 6 entries:

ν Low: 0 for the first band, left edge frequency for the others.
ν High: The Nyquist frequency (0.5*sampleRate) for the last band, high edge frequency for the others.
H: The ideal frequency response (gain).
W: A relative weighting.
- A value greater than 1 decreases the error in the band but increases the tolerance.
- A value smaller than 1 increases the error in band and decreases the tolerance.
nAlt: the number of alternations in each band for the initial solution. If Initialize from alternations is unchecked, the entry is disabled and the number of alternations is computed from target δ, the minimum cutoff width and the highest H value. If Initialize from alternations is checked, the target δ entry is disabled.
⚠ nAlt can change during iteration: an alternation can move from one band to another and alternations can be added if the algorithm detects it will help to get a converged solution.
The total number of alternation, that has numerical limitation, is displayed below the colum and the resulting filter order is 2⋅(nAlt - 2).
The Cut entry is disabled and displays the cutoff width.

⚠ Edge frequencies can move and cutoff width can change during iteration as shown in the slideshow below where the two central bands have the same gain H_i.

If Initialize from alternations is checked, you can define the number of alternations for the initial solution. In that case, target δ is ignored and the entry is grayed out. The number of alternation is derived from the Kaiser approximation available for a 2 bands filter nAlt=(-20 log₁₀(δ) - 13) ∕ (2.324 * cutoffWidth).

The above formula is modified in order to take into account that

the bandwidth (ν_hi − ν_li) is not the entire frequency range.
a band can be surrounded by 2 cutoff bands frequencies and, in that case, if both surrounding bands have a higher or lower gain that the considered band, the number of alternations is expected be odd. It is expected be even if one has a higher gain and the other a lower gain. ⚠ this is not always true since it can occur that edge frequencies are also extremals as in the previous example where two consecutive bands have the same gain.

Numerical parameters

δ allows you to enter the target tolerance which is the ripple amplitude when convergence is reached. In the entry beside, you can enter it in dB units. The value obtained by the iterative algorithm is displayed in the grayed out entry beside once the iteration process has started. ⚠ The δ entry is used only to estimate the number of alternations in each band when Initialize from alternations is unchecked. The entry is disabled if Initialize from alternations is checked.

nIt is the maximum number if Remez iterations.

ε is the convergence criteria. The algorithm is converged when the relative difference between the maximum and minimum ripple amplitudes is smaller than ε : (Emax − ∣δ∣) ∕ ∣δ∣ < ε. ⚠ It does not take into account extremals found between edge frequencies of two neighbour bands.

if Debug is checked, the , and h buttons are available in the button line and the error function is displayed in the DSP dialog.

if Scheme is checked, the tolerance scheme is shown in the DSP dialog.

if Expand is checked, cutoff frequencies are allowed to move outside the cutoff band. This allows to obtained converged solutions on test cases that otherwise freeze before reaching the convergence criteria as illustrated in the two first slides below where Expand is unchecked. When the cutoff frequencies move outward the cutoff bands as illustrated by the 3^rd and 4^th slides below, a warning message Cutoff frequencies have moved is printed in the DSP dialog. In that case, you should check the frequency response around the frequency values printed beside the warning if the frequency response lies inside the tolerance scheme as in the 3^rd slide or outside as in the 4^th one. The region where the frequency response is outside the tolerence scheme in the 4^th slide is not taken into account for the Emax value because there is no extremal in that region.
You can also improve solution by setting the number of alternation or adjusting your edge frequencies.

Buttons

Clicking the button opens a file chooser for selecting an equiripple design file (.eqrpl).

Clicking the button save the current design in a an equiripple design file (.eqrpl). If there is no file associated with the current design, a file chooser opens for selecting one.

Clicking the behaves as the button but a file choser opens in any case.

Clicking the button compute the initial solution. If Debug is checked, the alternations are computed and displayed as red dots for extremals and red crosses for edge frequencies. If there are too much extremals, the discarded ones are colored in blue. The extremals that lie inside cutoff bands and are not taken into account for the next iteration are colored in green.

Clicking the button go back to the previsous iteration. Only available if Debug is checked.

Clicking the button executes one iteration and compute the alternations at the end for displaying it with the error function. Only available if Debug is checked.

Clicking the button executes the Parks–McClellan algorithm until:

Convergence is reached. In the case, the impulse response is computed and a new filter is added in the DSP dialog.
Algorithm is frozen or looping without reaching convergence.
Algorithm failed: not enough alternation are found or numerical error occured.
The maximum number of iteration nIt is reached.

The h button allows yout to compute the impulse response and create a new filter in the DSP dialog when the algorithm did not converge but the solution is satisfactory.

Python commands

Here are the functions that can be called from Python scripts.

            # Initialize the band parameters from the 
            global parameters
            
DSPEquirippleFirCreateEquiBand(int shape,int nBand, float delta, float hMax, float hMin, float cutwidth)
            
# The shape parameter can be 0 (crenel), 1 (up-staire) or 2 (down-stairs).
            
# nBand is the number of bands.
            
###############################################################

        # Initialize equiripple filter with the band parameters
        
DSPEquirippleFirInit(int nBand, float f_1,...,float f_2*nBand,
        
  float h_1,...,float h_nBand,
        
  float w_1,...,float w_nBand, int nAlt_1, ..., nAlt_nBand ) 
        
# nBand is the number of bands.
        
# f_1,..., f_2nBand are the 2*nBand ege frequencies 
        
# with f_1 = 0, f_2nBand=0.5*sampleRate
        
# h_1,...,h_nBand are the band gains.
        
# w1, ...,w_nBand are optional. They are relative weightings.
        
# nAlt_1, ..., nAlt_nBand are the number of alternations used 
        
# only if Initialize from alternations is checked.
        
###############################################################

        DSPEquirippleFirIterate() # Iterate one step
        
###############################################################

        DSPEquirippleFirStepBack()# Go back to the previsous iteration.
        
###############################################################

        DSPEquirippleFirRun() # Execute the Parks-McClellan algorithm. 
        
#Returns filter name
        
###############################################################

        DSPEquirippleFirImpulseResponse() # Compute impulse response.
        
###############################################################

        #Set the target tolerance δ
        
DSPEquirippleFirSetDelta(float deltaTarget)
        
###############################################################

        #Set the covergence criteria ε
        
DSPEquirippleFirSetEpsError(float eps)
        
###############################################################

        #Set the maximum number of iterations
        
DSPEquirippleFirSetMaxIter(int maxIteration)
        
###############################################################

        # Check/uncheck the Initialize from alternations
        
# checkbox:  true if i != 0, false otherwise
        
DSPEquirippleFirInitFromAlternations(int i)
        
###############################################################

        # Check/uncheck the Debug mode.
        
# true if i != 0, false otherwise
        
DSPEquirippleFirSetDebugMode(int i);
        
###############################################################

        # Check/uncheck Expand cutoff bands.
        
# true if i != 0, false otherwise
        
DSPEquirippleFirAllowExpandCutoff(int i);
        
###############################################################

        # Check/uncheck tolerance scheme.
        
# true if i != 0, false otherwise
        
DSPEquirippleFirShowScheme(int i);
        # true if i != 0, false otherwise
        
###############################################################

        # Open the equiripple design file (.eqrpl) fileName .
        
DSPEquirippleFirOpenFile(string fileName);
        
###############################################################

        # Save the current equiripple design.
        
# Fails if it is not currently associated with a file 
        
DSPEquirippleFirSaveFile();
        
###############################################################

        # Save the current equiripple design to file (.eqrpl) fileName.
        
DSPEquirippleFirSaveFileAs(string fileName);
        
###############################################################

        # Close the Equiripple dialog
        
DSPEquirippleFirClose()
        
###############################################################